日志
物理学家可能是AI时代最后躺平的
热度 2 ||
神经网络不是统计,它是在构造一个巨大的逻辑函数。这你从下围棋就知道了。你下哪,AI能够给出对应的下法,IF THEN ELSE. 即使不去搜索下一步,AI也比大部分人强。训练过程不需要逻辑,只是数据迭代。训练出来是神经网络本身具备了逻辑。这跟人是类似的,教小孩说话、思考不需要教逻辑,小孩跟着学久了,就开窍了。AI完全自学,AI下围棋是从零开始,连规则都没有输入,然后自己通过对弈,学会规则,并且达到超人的水平。那个用人类棋谱训练的版本是跟李世石下的版本,李世石还赢了一盘。之后,AI自学成才,人就没再赢过。AI针对性训练,人也一样,从小训练中文还是德语,看四书五经还是康德。现在AI把这些书都看完了,而且看懂了。这个看书过程完全是自主进行,没有任何提示,看多了,它就顿悟了。这其实不奇怪,有些关系不需要 AI 就能得出来。比如说,光是通过向量代数,程序就能在看完书后, 就得出 queen = king - man + woman,巴黎=北京-中国+法国,等等。这完全不需要AI,是一个固定算法。一个词用一个多维向量表达,开始这些向量都设为0, 这个简单的程序在处理一些书籍的内容之后,就得出了不同词之间的向量关系。AI 自学则是可以自己学通书表达的知识。
下棋、玩游戏这些对AI早就是小意思了。ChatGPT-4 参加美国法学院入学考试 LSAT,成绩超过 88% 的考生;ChatGPT-4 进行美国律师资格考试成绩超过了 90% 的参试者 --那些在美国读完大学、然后贷款进法学院学习三年、出来背一身债的人们;ChatGPT-4 进行生物奥利匹克测试,成绩超过 99% 的人;ChatGPT-4 进行 SAT 阅读写作测试,成绩超过 93%的人;在 SAT 数学部分,它的成绩超过 89% 的人。其余测试,如微积分、化学、医学, ChatGPT-4也都有出色表现。成绩单中唯一空白的是物理。
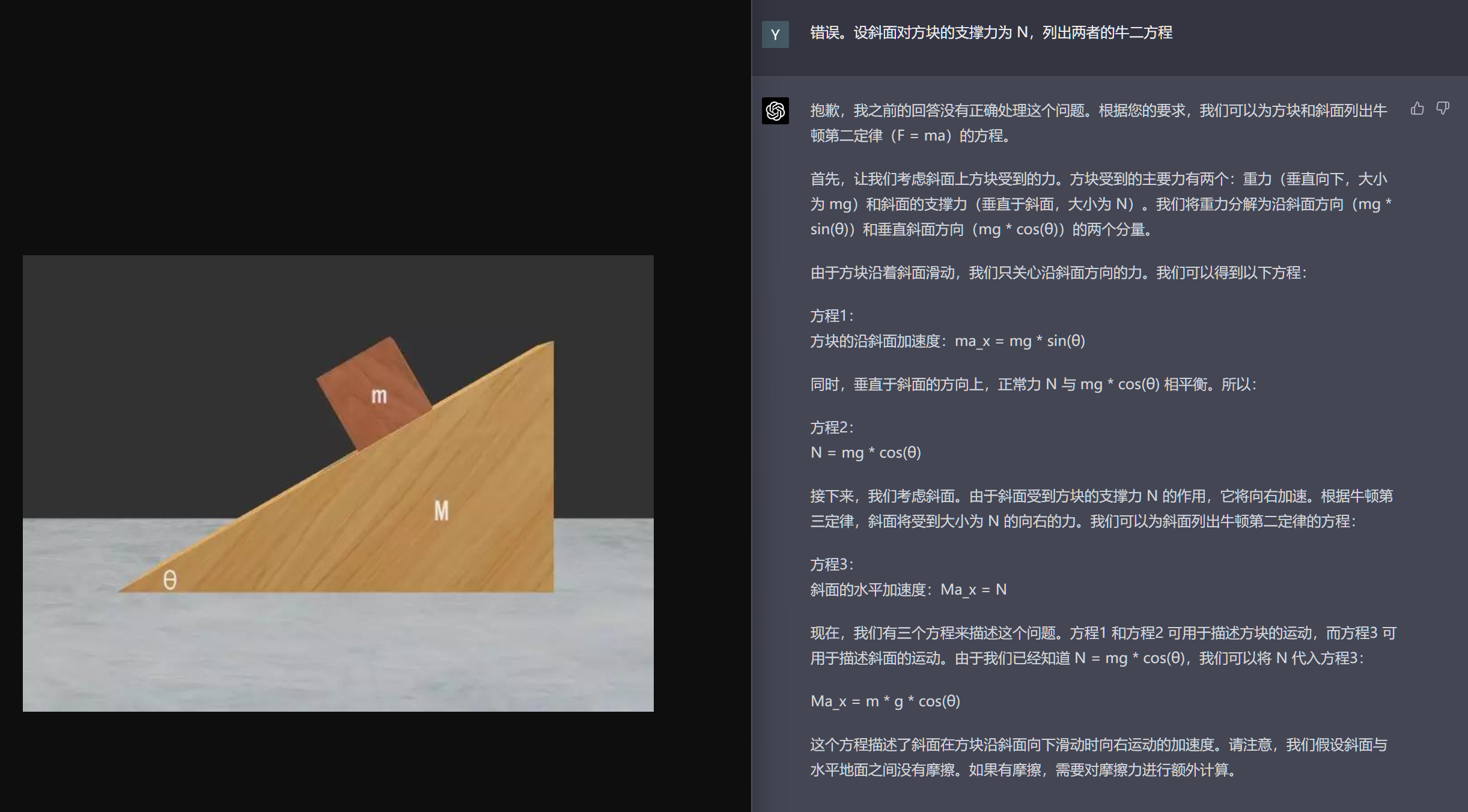
我对 ChatGPT-4进行了几个物理测试。 简单的电路能看懂,但稍微复杂一点的力学就不会了。这个斜面置于光滑水平面,方块从光滑斜面滑下,计算斜面后退加速度的问题,即使经过提示,它还是做不对。这个力学问题难在哪呢?它必须明白,因为斜面在加速后退,不能直接以斜面为参照列出牛顿方程(注)。看来要 AI 弄明白这个物理关系,光是语言(符号关系)还不行。
为什么不同学科 ChatGPT 这个水平差异这么大呢?前面那些科目都是相对固定的。记忆+直线推理就差不多了。物理不同。一个稍微变化一点的物理问题,其实需要测试者本身提出问题、构造问题,然后才是解决问题。物理思维在一个更高的层次。以那个斜面上的方块下滑的问题为例,如果斜面不动,那是一个固定套路,AI毫不费力。如果斜面本身可以滑动,这也是个中学物理题,中学物理稍微好点的学生会做。ChatGPT-4 虽然知道斜面会滑动,但它无法正确地运用牛顿第二定律列出相关的 F=ma 方程。实际上,这个列方程是一个提出问题、构造问题的过程。一旦这一步解决了,解方程就是直线逻辑了。
注:我后来让 ChatGPT 写出以方块以斜面上的位置s与斜面自身位置 x为广义坐标 的拉格朗日量,它算是写对了,然后让它推导运动方程也是程序化的。