日志

泰坦号深潜器爆缩时间的计算

热度 1已有 3666 次阅读2023-7-9 08:21 |个人分类:科普|系统分类:科普

6月18日，美国民间企业 OceanGate 一艘名为泰坦号的深潜器在加拿大纽芬兰附近的大西洋洋面深潜探险时失联。搜救人员在离泰坦尼克沉船约500米处发现了泰坦号的残骸，判断该深潜器发生内爆 -- 在外部巨大的压强下深潜器载人舱被压扁。在4000米的深度压强大约400个大气压。现在的问题是这个内爆有多快？我看了网上不少分析，YouTube 有几个冗长的分析说是计算得出水压下崩塌速度达到两倍音速，完成时间只有一毫秒。下面，我用牛顿力学进行简单的分析，结论是时间约为10毫秒。

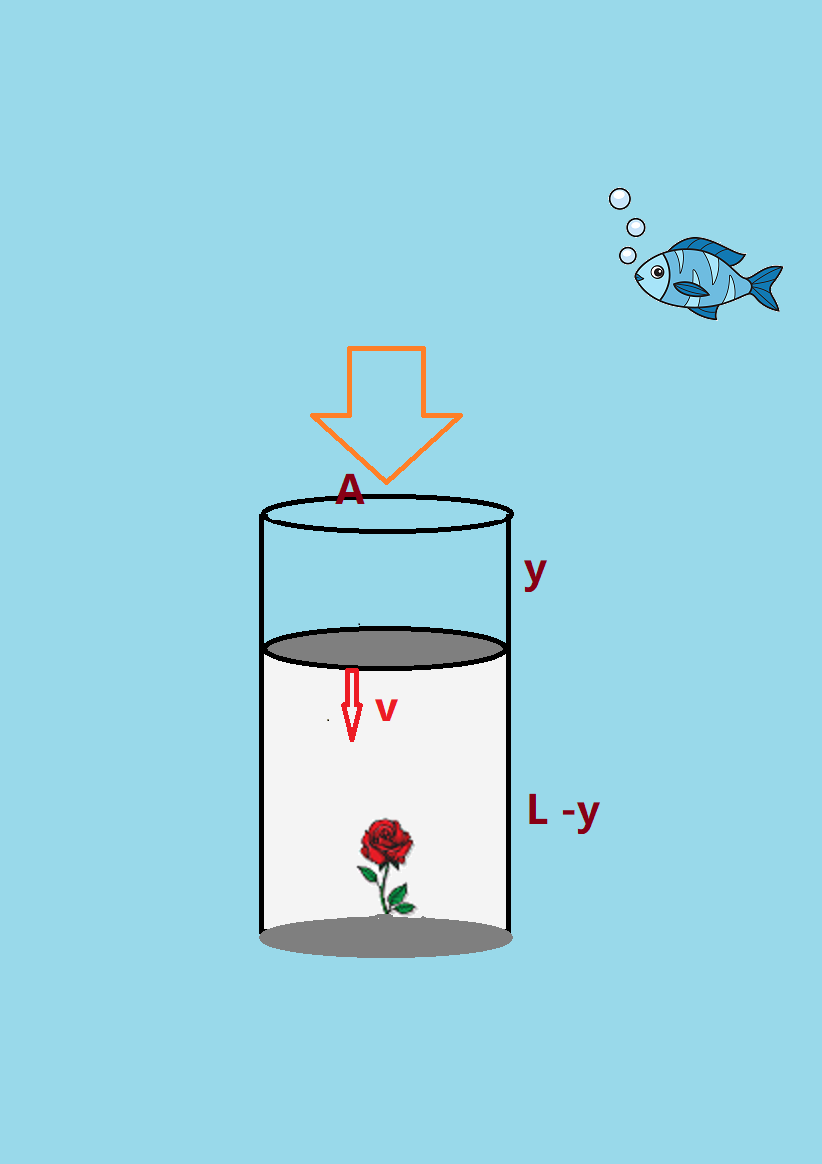
我们的模型是，一个长度为 L，横截面积为A 的圆柱容器放在深度为 H 的水中（H >> L）。突然，在 t=0 时刻，这个圆柱容器的质量为 M 的顶盖完全失去支撑，这使它在外部水压下向下行，在时间 t 其下行距离为 y(t)。我们需要知道的是顶盖下行速度 v 是多少。

在泰坦号这个具体问题里，由于水深达 4000米，压强达 400大气压，而艇内只有一个大气压，我们暂时忽略艇内空气的压力，同时我们假设顶盖质量 M 可以忽略，那么问题简化为一段长度 y 的水柱在下行。这类似一个中学物理里常见的一个问题，在水桶下方钻个小孔，请问水流速度是多少。在这里，压入圆柱的水柱的动能等于系统的势能的减少。由于这个变化相当于从水面取走等量的水压入圆筒内，压入水柱的速度也就等于从 H 高度自由落体的速度，也就是 [ix] v= \sqrt{2gH}[/ix]。代入H=4000m, g =9.8, 我们得到 v~ 280 (m/s)。也就是说，在这个4000米深度，当圆筒顶盖突然失去支撑，它将水压下以每秒280米的速度下压。这个水流速度没有超过音速。泰坦号载人舱长度只有 2.5 米。按这个速度只有约 1/100 秒的压缩时间。里面的人是来不及感知这一切的。

读者可能会问，既然水被压入圆筒，那整个水体都在下行，在上面能量守恒的计算中为什么不考虑整个水体下行的动能呢？这是因为水整体下行的速度正比于圆柱截面积 A 与水体表面积 B 的比，尽管水体质量正比于 B，但动能正比于（A/B）的平方。对于海洋来说，因此这部分动能显然在计算中忽略（如果是在一个面积不大的深水池，水面整体下降的动能不能忽略，那将减少冲入圆筒的水流速度。）

当然，下行水柱不可能瞬间达到 280 m/s 的速度，因此实际时间还要长一点。我们要计算这个过程就得正确使用牛顿第二定律了。中学物理学的牛顿第二定律方程是 F=ma。其实它正确的表达、也是牛顿《自然哲学之数学原理》一书中的表达是 F = dp/dt ，外力等于系统动量的变化率。这里，压入圆筒内的水柱的质量是在增加的，F=ma不能用，得用 dp/dt。具体计算很复杂。下面是一个 handwaving 的估计。

长度为 y 的水柱质量 m = \rho A y，其中 \rho 为水的密度， v = dy/dt。因此顶盖与水柱的动量为 [ix]（M + \rho A y）dy/dt[/ix] 。圆筒口处等效水压强为 [ix] c \rho g H[/ix]，c 为常数。牛顿第二定律方程为：

[ix] c \rho g H A = d((M + \rho A y ) \frac{dy}{dt})/dt[/ix]

初始条件 t=0, y=0, v=0 (冲量等于动量变化)

[ix]c \rho g H A dt = d ((M + \rho A y ) \frac{dy}{dt})\\ \rho g H A t = (M + \rho A y ) \frac{dy}{dt}[/ix]

再分解变量：

[ix]c \rho g H A t dt = (M + \rho A y ) dy[/ix]

也就是

[ix] c \rho g H A t dt = (M + \rho A y ) dy\\ \rho g H A t^2 + C = 2 M y + \rho A y^2 [/ix]

根据初始条件 t=0, y=0, v=0，确定 C =0

[ix] \rho A y^2 + 2 M y - c \rho g H A t^2 =0 \\ y^2 +\frac{2 M}{\rho A} y - c gH t^2=0[/ix]

对比上面能量守恒的结果，我们得出 c = 2 。

从 [ix]y^2 +\frac{2 M}{\rho A} y - 2 gH t^2=0\\t = \sqrt{\frac{y^2+\frac{2M}{\rho A}}{2gH}}[/ix]

设盖子厚度为0.2米，密度为水的4倍, 代入 y = 2.5 (m)，我们得到

[ix] t = \sqrt{\frac{y^2+\frac{2M}{\rho A}}{2gH}}= \sqrt{\frac{2.5^2+1.6^2}{2\times 9.8 \times 4000}} \approx 0.011 (second)[/ix]

与最初的估算结果非常接近。

有人说，在水柱抵达前，空气先被压缩到高温，人被气化了。这是不成立的，温度不等于能量，深潜器里也没有足够氧气支持燃烧。这个过程非常迅速不能使用平衡态的气体方程进行分析。大概的物理过程是水柱前锋推动临近气体以水速的两倍速度迅速向舱内运动，在舱室另一端反弹，如此来回往复，这个时间尺度比水流快一倍，但由于空气密度小，不会在这么短时间内造成死亡。