日志
太阳系模拟(含哈雷彗星)-- ChatGPT 编程
||
solar-chat-gpt——使用Clipchamp制作.mp4
1677年,牛顿用拉丁语写了一本 《Philosophiæ Naturalis Principia Mathematica》,里面充斥着各种几何图形,没有用到任何微积分。为了解决一个现在看来简单的力学问题,牛顿必须证明各种几何定理、引理。100年后的1788 年,法国(意大利裔)数学家拉格朗日写了一本《Mécanique Analytique》(《分析力学》),他自豪地说,全书没有一张图。解决牛顿力学问题往往需要相当好的物理概念,要知道向量等概念,要进行受力分析之类。但使用分析力学方法,你只需要写下一个称为拉格朗日量的标量,剩下的就是计算。后人在其基础上又发展出哈密顿力学。你只要写出系统的能量 H,接下来就是两个一阶方程, q' = dH/dp, p' = -dH/dq,几乎不要动脑筋,硬算即可推导出系统的演化。
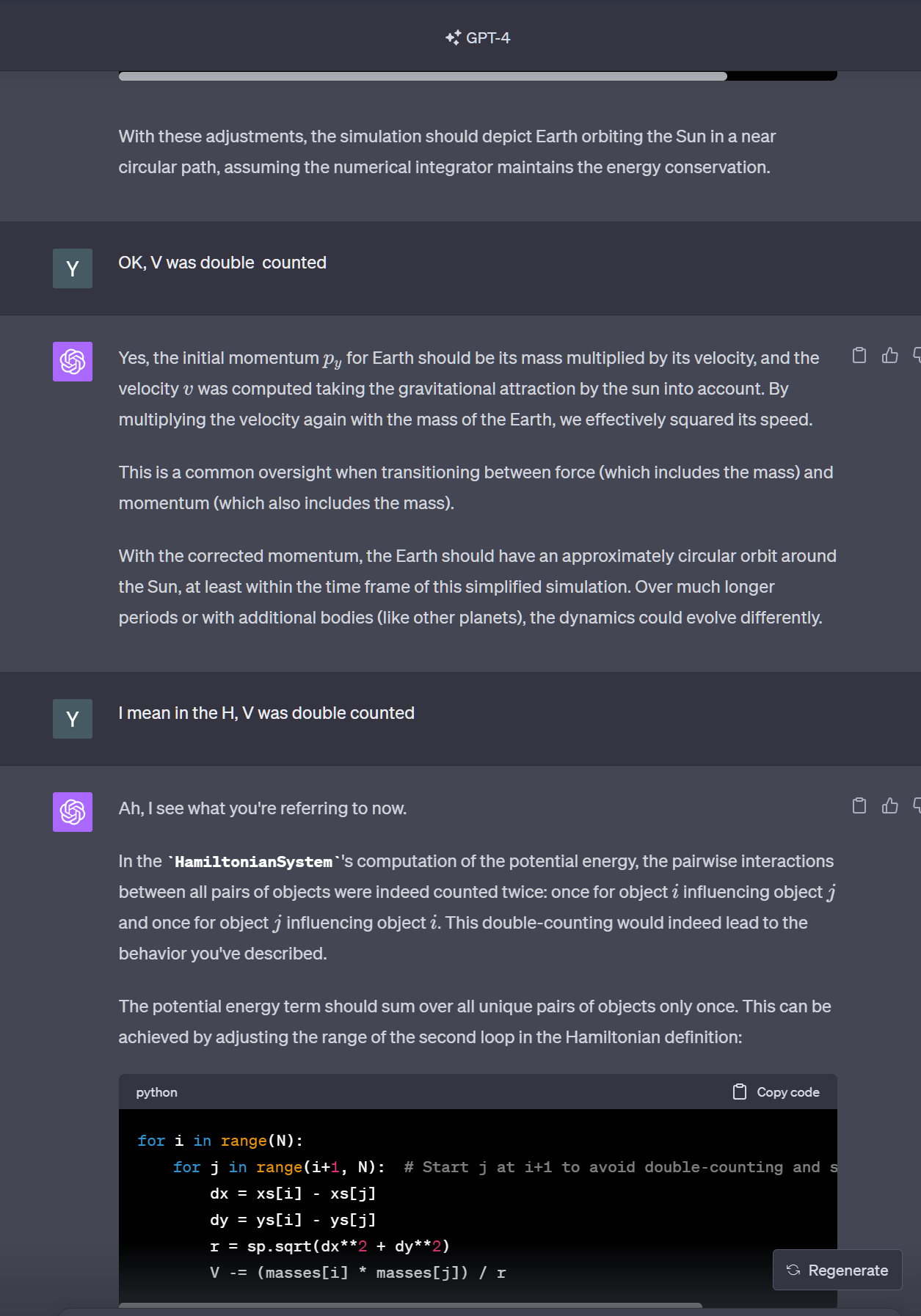
ChatGPT 自从推出以来,其能力水平大有提高,但我前天测试一下,它还是不能正确解决那个物体从斜面滑下、斜面后退、请计算加速度的中学力学题。但我突然想起何不让它用哈密顿力学算一下太阳系的运动。ChatGPT 看到我的提示,毫不犹豫的开始写代码。一次运行畅通无阻,但我发现地球的轨道不对,一年没有回到起点。我查看了一下,ChatGPT 在算星体之间的引力能时算了两次,A与B,然后是 B与A。于是我提示到 H 里 V 算重了,就这么个提示,ChatGPT 立刻知道了问题所在,而且立刻修改了代码。这不得不令人赞叹。(代码附在文末)
视频是太阳系运转图。从水星到火星,到太阳的距离比例是对的。但从木星开始,距离显示进行了比例缩减。那个白色的是哈雷彗星。

import sympy as sp
# The Hamiltonian system definition as above...
class HamiltonianSystem:
def __init__(self, N):
self.xs = sp.symbols(f'x0:{N}')
self.ys = sp.symbols(f'y0:{N}')
self.pxs = sp.symbols(f'px0:{N}')
self.pys = sp.symbols(f'py0:{N}')
self.ms = sp.symbols(f'm0:{N}')
T = sum(self.pxs[i]**2 / (2 * self.ms[i]) + self.pys[i]**2 / (2 * self.ms[i]) for i in range(N))
V = sum(-self.ms[i] * self.ms[j] / sp.sqrt((self.xs[i] - self.xs[j])**2 + (self.ys[i] - self.ys[j])**2)
for i in range(N) for j in range(i+1, N) if i != j)
self.H = T + V
self.H_numeric = lambdify((*self.xs, *self.ys, *self.pxs, *self.pys, *self.ms), self.H)
def dHdx(self, i):
return sp.diff(self.H, self.xs[i])
def dHdy(self, i):
return sp.diff(self.H, self.ys[i])
def dHdpx(self, i):
return sp.diff(self.H, self.pxs[i])
def dHdpy(self, i):
return sp.diff(self.H, self.pys[i])
def H_value(self, states, masses):
N = len(states)
# Separate states for easy referencing
x = [states[i][0] for i in range(N)]
px = [states[i][1] for i in range(N)]
y = [states[i][2] for i in range(N)]
py = [states[i][3] for i in range(N)]
# Use the lambdified function
return self.H_numeric(*x, *y, *px, *py, *masses)
# The numerical simulation as above...
from sympy import lambdify
class NumericalSimulation:
def __init__(self, N, masses):
self.system = HamiltonianSystem(N)
self.masses = masses
self.dHdx_funcs = [lambdify((*self.system.xs, *self.system.ys, *self.system.pxs, *self.system.pys, *self.system.ms),
self.system.dHdx(i)) for i in range(N)]
self.dHdy_funcs = [lambdify((*self.system.xs, *self.system.ys, *self.system.pxs, *self.system.pys, *self.system.ms),
self.system.dHdy(i)) for i in range(N)]
self.dHdpx_funcs = [lambdify((*self.system.xs, *self.system.ys, *self.system.pxs, *self.system.pys, *self.system.ms),
self.system.dHdpx(i)) for i in range(N)]
self.dHdpy_funcs = [lambdify((*self.system.xs, *self.system.ys, *self.system.pxs, *self.system.pys, *self.system.ms),
self.system.dHdpy(i)) for i in range(N)]
def step(self, states, dt):
N = len(states)
# Separate states for easy referencing
x = [states[i][0] for i in range(N)]
px = [states[i][1] for i in range(N)]
y = [states[i][2] for i in range(N)]
py = [states[i][3] for i in range(N)]
for i in range(N):
px[i] -= 0.5 * dt * self.dHdx_funcs[i](*x, *y, *px, *py, *self.masses)
py[i] -= 0.5 * dt * self.dHdy_funcs[i](*x, *y, *px, *py, *self.masses)
for i in range(N):
x[i] += dt * px[i] / self.masses[i]
y[i] += dt * py[i] / self.masses[i]
for i in range(N):
px[i] -= 0.5 * dt * self.dHdx_funcs[i](*x, *y, *px, *py, *self.masses)
py[i] -= 0.5 * dt * self.dHdy_funcs[i](*x, *y, *px, *py, *self.masses)
# Repack the states
new_states = [(x[i], px[i], y[i], py[i]) for i in range(N)]
return new_states
def energy(self, states):
return self.system.H_value(states, self.masses)
import numpy as np
class SymplecticIntegrator:
def __init__(self, dHdx_funcs, dHdy_funcs, masses):
self.dHdx_funcs = dHdx_funcs
self.dHdy_funcs = dHdy_funcs
self.masses = masses
# Coefficients for 2nd order method
self.c2 = [0, 1]
self.d2 = [0.5, 0.5]
# Coefficients for 3rd order method
self.c3 = [1, -2/3, 2/3]
self.d3 = [-1/24, 3/4, 7/24]
# Coefficients for 4th order Yoshida method
t13 = np.power(2, 1/3)
self.c4 = [1 /(2* (2-t13)),
(1-t13)/2/(2-t13),
(1-t13)/2/(2-t13),
1 /(2* (2-t13))]
self.d4 = [1 / (2-t13),
-t13/(2-t13),
1 / (2-t13),
0]
def position_step(self, x, px, y, py, dt, c):
N = len(x)
for i in range(N):
x[i] += dt * c * px[i] / self.masses[i]
y[i] += dt * c * py[i] / self.masses[i]
return x, y
def momentum_step(self, x, px, y, py, dt, d):
N = len(x)
for i in range(N):
px[i] -= dt * d * self.dHdx_funcs[i](*x, *y, *px, *py, *self.masses)
py[i] -= dt * d * self.dHdy_funcs[i](*x, *y, *px, *py, *self.masses)
return px, py
def step(self, states, dt, order=2):
N = len(states)
x = [states[i][0] for i in range(N)]
px = [states[i][1] for i in range(N)]
y = [states[i][2] for i in range(N)]
py = [states[i][3] for i in range(N)]
if order == 2:
coeffs = zip(self.c2, self.d2)
elif order == 3:
coeffs = zip(self.c3, self.d3)
elif order == 4:
coeffs = zip(self.c4, self.d4)
else:
raise NotImplementedError(f"Order {order} not implemented.")
for c, d in coeffs:
x, y = self.position_step(x, px, y, py, dt, c)
px, py = self.momentum_step(x, px, y, py, dt, d)
new_states = [(x[i], px[i], y[i], py[i]) for i in range(N)]
return new_states
import pygame
import sys
import math
import os
# Test code as requested...
v_earth = 29.78 #km/s
G = 6.67430e-11 # gravitational constant in m^3 kg^−1 s^−2
M = 1.989e30 # mass of the Sun in kg
r = 0.586 * 1.496e11 # distance from the Sun at perihelion in meters
a = 17.83 * 1.496e11 # semi-major axis in meters
v_haley = math.sqrt(G * M * (2/r - 1/a))/v_earth/1000
print(f"vh={v_haley}")
# Normalized masses based on the mass of the Sun set to 1
mass_sun = 1
mass_earth = 3e-6
mass_mercury = 1.66e-7
mass_venus = 2.45e-6
mass_mars = 3.3e-7
mass_jupiter = 9.55e-4
mass_saturn = 2.86e-4
mass_uranus = 4.37e-5
mass_neptune = 5.15e-5
mass_haley = 1e-8
masses = [mass_sun, mass_mercury, mass_venus,mass_earth, mass_mars, mass_jupiter, mass_saturn, mass_uranus, mass_neptune, mass_haley]
# Normalized distances from the sun (in AU) and velocities with Earth's set to 1
earth = (1, 0, 0, mass_earth) # Earth's velocity is the reference (momentum in y-direction)
mercury = (0.39, 0, 0, mass_mercury * 1.61) # Orbital velocity normalized to Earth's
venus = (0.723, 0, 0, mass_venus * 1.18)
mars = (1.524, 0, 0, mass_mars * 0.81)
jupiter = (5.203, 0, 0, mass_jupiter * 0.44)
saturn = (9.537, 0, 0, mass_saturn * 0.33)
uranus = (19.191, 0, 0, mass_uranus * 0.23)
neptune = (30.069, 0, 0, mass_neptune * 0.18)
haley = (0.586, 0,0, v_haley*mass_haley)
sun_p= - sum(s[3] for s in [mercury, venus,earth, mars, jupiter, saturn, uranus, neptune, haley])
sun = (0, 0, 0, sun_p) # Sun stays stationary
states = [sun, mercury, venus,earth, mars, jupiter, saturn, uranus, neptune, haley]
sim = NumericalSimulation(len(masses), masses)
stepper = SymplecticIntegrator(sim.dHdx_funcs, sim.dHdy_funcs,masses)
dt = 0.01
num_steps = 628 # For example, this evolves the system for 10 units of time
# for _ in range(num_steps):
# state = sim.step(states, dt)
# total_energy = sim.system.H_value(states, masses)
# print(f"Total energy of the system: {total_energy}")
# #print(f"Position of object 1: ({x[0]}, {y[0]})")
# print(f"Position of object 2: ({state[1][0]}, {state[1][2]})")
# Initialize pygame
pygame.init()
# Screen settings
WIDTH, HEIGHT = 1800, 1800
screen = pygame.display.set_mode((WIDTH, HEIGHT))
pygame.display.set_caption("Solar System Visualization")
clock = pygame.time.Clock()
# Colors
WHITE = (255, 255, 255)
YELLOW = (255, 255, 0) # Sun
COLORS = [
(139, 69, 19), # Mercury: brown
(245, 123, 0), # Venus: pink
(0, 0, 255), # Earth: blue
(255, 0, 0), # Mars: red
(255, 165, 0), # Jupiter: orange
(210, 105, 30), # Saturn: chocolate
(64, 224, 208), # Uranus: turquoise
(0, 0, 128), # Neptune: navy
(125,125,125)
]
# Sizes
SUN_SIZE = 30
PLANET_SIZES = [8, 12, 15, 12, 25, 20, 18, 17,18] # Adjust as needed to visualize comfortably
GRADIENT_RAYS=30
pygame.font.init()
font = pygame.font.SysFont(None, 20)
def display_energy(screen, steps, energy):
# Initialize the font system (can be done once at the start of the program)
# Render the text
text_surface = font.render(f"Total Energy: {energy:.2f}", True, (255, 0, 255)) # White color
# Display the text at the top left corner
screen.blit(text_surface, (10, 10))
text_surface = font.render(f"Years: {steps/628.0:0.2f}; Steps: {steps}", True, (255, 0, 255)) # White color
# Display the text at the top left corner
screen.blit(text_surface, (10, 32))
def draw_star(screen, color, center, radius, edge=1):
pygame.draw.circle(screen, color, center, radius)
edge_color = [int(c/2) for c in color]
# Draw gradient rings
for i in range(1, GRADIENT_RAYS + 1):
alpha_value = 255 - i * (255 // GRADIENT_RAYS)
color_with_alpha = tuple(edge_color) + (alpha_value,)
# Create a temporary surface for this specific ring
ring_radius = radius + i * edge
ring_thickness = edge
temp_surface = pygame.Surface((WIDTH, HEIGHT), pygame.SRCALPHA)
# Draw the outer circle of the ring
pygame.draw.circle(temp_surface, color_with_alpha, center, ring_radius)
# Mask out the inner part to only leave the fading edge (ring) visible
mask_color = (0, 0, 0, 0) # fully transparent
pygame.draw.circle(temp_surface, mask_color, center, ring_radius - ring_thickness)
screen.blit(temp_surface, (0, 0))
# Positions (here we're just starting them at their initial distances, you'll want to update this dynamically based on your simulation)
LOG_BASE = 1.5
running = True
scale = WIDTH/5/2
steps=0
while running:
for event in pygame.event.get():
if event.type == pygame.QUIT:
running = False
screen.fill((0,0,0))
# Drawing Sun
states = stepper.step(states, dt,order=3)
steps +=1
positions = [(s[0], s[2]) for s in states]
total_energy = sim.system.H_value(states, masses)
#print(f"Total energy of the system: {total_energy}")
draw_star(screen, YELLOW, (positions[0][0]*scale+WIDTH/2, positions[0][1]*scale+HEIGHT/2), SUN_SIZE)
# Drawing planets
for idx, position in enumerate(positions[1:]):
x, y = position
d = math.sqrt(x*x+y*y)
#dl = math.log(d+1, LOG_BASE)
dl=d
if d>2:
dl = 2+(d-2)/8
x = x/d *dl*scale+WIDTH/2
y = y/d *dl*scale+HEIGHT/2
pygame.draw.circle(screen, COLORS[idx], (x,y), PLANET_SIZES[idx])
display_energy(screen, steps, total_energy)
#imgpath = os.path.join("k:/tmp/solar/", f"{steps:05d}.png")
#pygame.image.save(screen, imgpath)
pygame.display.flip()
clock.tick(100)
# If you're running a simulation, update the positions here...
pygame.quit()
sys.exit()







